Abstract time

Of course it is reasonable for someone to say "to find the divergence of the electric field, integrate over this closed service", or "to find the mass density, integrate over this volume", but what exactly do we integrate when we integrate over time? How do we define what it is that we are integrating over? And more importantly, how can we determine when we find some physics that is this integral of time?

If any physical process were to change in the same manner and magnitude as time itself, it would remain completely imperceivable to those in motion through this temporal dimension at the same rate as that process. If space itself were to dilate with time and our experience of time is this spatial dilation, how would we detect it if the devices we use to measure length rely on the underlying space that is now dilated? If one meter grows to two meters in one instance of some time equivalent, but everything around us, including our meter stick also scales by a factor of 2, how would we then measure this dilation?

Of course this notion falls apart if this, or any physical process dilates in a manner that is not equivalent to the nature of time, both in magnitude and in the quantity being modified, but what if we have detected this phenomenon centuries ago and are just now to understand it?

Mechanics without an explicit time dimension

Before moving forward, we should lay out some simple mathematics for deriving mechanics and simultaneity without an explicit time dimension. There exists many more time equivalent quantities that can be derived from various descriptions of motion, but these will suffice for what we are undertaking here.

Proportional Derivatives

What is meant by proportional derivatives is that for any infinitesimally small value there should be another derivative, that is equivalent to . This allows us to treat velocities as pure vectors when dealing with gravity, the proposed physical expression of time, without including an abstract time dimension. By integrating these vectors simultaneously, especially when working with paths of a finite length, we can produce the same notion of simultaneity and even temporal progression that occurs in classical and relativistic physics without any dependence on an abstract temporal axis. When integrating these proportional derivatives here, I will use a notation to indicate the proportional, simultaneous nature of their action.

The notion of proportional simultaneous integration¹ simply describes the concept of moving some body a distance of , at the same pseudo-time as all other bodies in motion according to their own proportional velocity derivatives. It is however important to recognize that the notion of time here is entirely mathematical, and in no manner describes anything inherent to the system. This process is almost entirely analogous to integrating over time apart from the fact that we can now do so without dependence on an actual temporal dimension; a quantity which we have no means to measure directly, and which I propose, does not actually exist in any classical or even relativistic sense. However, when addressing proportional simultaneous integrals in relation to gravitational acceleration this distinction becomes critical, as this apparent acceleration acts as the underlying mechanism of time in the model being proposed and must be integrated along with all proportional velocity derivatives. This is to say that for a temporal progression equivalent to a single pseudo-time derivative, every in a given system should progress according to each proportional velocity derivative as the surrounding space likewise dilates as a function of the sum of these proportional velocity derivatives, where runs over all bodies within the system.

Note that simultaneity can be found for two proportional simultaneous integrals (PSI)¹ when

where represents a small portion of the path of , and represents a derivative of the motion of as proportional to the derivative of the motion of , .

Time Equivalent Quantities

As many existing formulas that might be of interest reference this abstract time dimension directly, we should define a time equivalent quantity that follows the model described here, but has no explicit time dependence and is proportional to our existing measures. Of course is one such time equivalent quantity, but there exists many others for various types of motion, oscillations, and other time dependent functions.

As itself is time dependent, we should note here that is not velocity in the traditional sense, but rather the proportional integral of some over , where in turn is the distance equivalent of one unit of time for that velocity. In other words, if , but will grow proportionally to the progression of pseudo-time, where as will remain fixed at unit of pseudo-time.²

It is my proposition that this is the role which time has played for our mathematics to this point. It does not appear that we are removing a quantity that is an inherent part of physics itself, but rather that we are reformulating a useful mathematical tool developed centuries ago to more accurately model the processes we are attempting to describe.

Time derivative equivalent

Consider that for unit of pseudo-time will pass³. Because the passage of pseudo-time is defined by the relationship between proportional derivatives and distances, where indicates 1 unit of pseudo-time in units applied to the traditional notion of velocity, we can easily infer the following:

This gives time derivatives per unit of time, but more importantly, a time derivative, that is proportionate to if is defined by .

On the Pound Rebka results

As the famed Pound Rebka1 experiment compared velocities to the apparent acceleration of gravity, let us examine how this time equivalence is contained in their results.

Recall that the velocity they found through the relative motion of the emitter with respect to the receiver along a path normal to the Earth's surface was roughly

If we consider this experiment in the context of the time equivalent quantities described above, we should find that

As is proportional to in the traditional sense when considering local gravitational parameters, we can describe as:

We then find:⁴

This in turn produces the Pound-Rebka results as:

3-vector simultaneity

Special relativity produces an invariant 4-vector⁵, but what if we could collapse this 4-vector into pure space components, while still accounting for time and the dilation of time inherent to our existing models? The 3-vectors being proposed have an identical magnitude between reference frames in their derivative form, but the time component is now unnecessary to describe the system in question as displacement vectors are integrated over an elongated trajectory in the reference frame in motion. This in some sense breaks down the invariant nature of relativity based 4-vectors, but in turn produces a synchronicity that remains consistent between reference frames. While 3-vectors remain invariant in the model being proposed, the integral of becomes longer, in turn scaling the time elapsed over this integral by or a gravitational equivalent.

Simultaneity among relativistic 3-vector integrals

Consider two observers, and . If were to say to "move at precisely this velocity between this lighthouse and this clock-tower", how can it be that would arrive at this clock-tower in a time other than ? Existing models dilate both time and velocity in accordance with the Lorentz tensor, but then is no longer traveling at the agreed upon velocity . after all is the only variable either or have any direct influence over, apart from their ability to pick two arbitrary points in space; the lighthouse and the clock-tower in this example. While it is sensible to infer that velocities might appear different in different reference frames, it is unreasonable to conclude that and can not agree upon a magnitude of velocity when they themselves are determining this magnitude.

If does travel at precisely velocity , and in the reference frame of is equivalent to in the reference frame of yet the experimentally confirmed factor must be applied to the elapsed period between the lighthouse and the clock-tower, must be applied to space; not time. Of course the elapsed period also extends by a factor of , but this is only a matter of the lighthouse and clock-tower being further separated in the coordinate system of than in that of , lengthening the integral of by a factor of .

The equivalence principle

The equivalence principle, in which the force experienced on an accelerating platform in the direction of acceleration is believed to be indistinguishable from the force of gravity on the surface of a gravitational source if both are of the same magnitude, was foundational to Einstein's general theory of relativity. What if this equivalence principle is more than just a useful mathematical symmetry with mysterious origins, what if there is a physical mechanism for this equivalence?

In order to address this potential mechanism, we need to first describe the space which we are working in. The Universe is widely accepted to be expanding; we can measure this by calculating the Doppler shift produced by relative motion from stars and certain cosmic events at various distances. What is on the other side of this expansion is largely insignificant for this portion of the model being proposed, but there must exist something that encompasses this expansion. Even if this external space exists only in the mathematical sense, we can imagine a coordinate system that encompasses our expanding Universe. If the Universe were a blueberry muffin expanding as it bakes, this external space would be the interior of the oven. From here forward, I will refer to this space as space, and the expanding space of the Universe itself as space.

If we allow that this space encompasses our expanding Universe, barring any motion of the center of mass of the Universe within this space, there should exist one point at which a coordinate in space and a coordinate in space have no relative motion between them. We will calculate all velocities with respect to this point in space which I will now call , making velocities in some sense absolute, but still maintaining Einstein's dependence upon relative motion by using this shared fixed position as our reference frame.

as the source of the equivalence principle

Let us now consider as it would be applied to space. Where is the speed of light and some velocity, is found to be

Consider now that this dilation, if applied to space, might be the source of the equivalence principle. The equation for gravitational acceleration is found to be

If we differentiate this with respect to , this becomes

in the frame of the body in motion

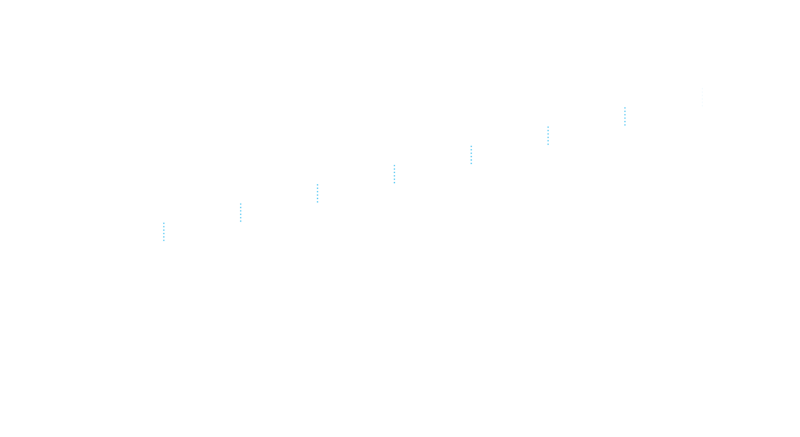
Let us now apply in a manner such that the dilation of space would produce a physical phenomenon equivalent to that which we experience as gravity. If instead of describing this dilation of space as a rate of change with respect to time, we might describe this dilation as a rate of change with respect to the change in displacement for the center of mass of the gravitational source.

As demonstrated in figure 1:

We can then describe this gradient, as a function of pseudo-time (the progression of ). As the rate of spatial dilation can be referenced using the original spatial density, , we combine these principles to arrive at:

Note here that gives a change in spatial dilation per change in displacement, and progresses this rate of change with pseudo-time; the proportional integral of the displacement vector of the center of mass of the gravitational source as proportionate to a distance-time equivalent⁶ quantity of .

If we now solve for , and replace with , we find the following:⁷

Note that is equivalent to if ⁸. Likewise, if , making this equation reducible to the following when applied over a single unit of pseudo-time:

The Earth's polar radius was used in the calculation above. Using the Earth's equatorial radius reduces the discrepancy between this result and the velocity derived from observational data with respect to the CMB dipole to , while using a radius derived from the standard acceleration of gravity produces a median error of .

Orbital velocity without an explicit time dimension

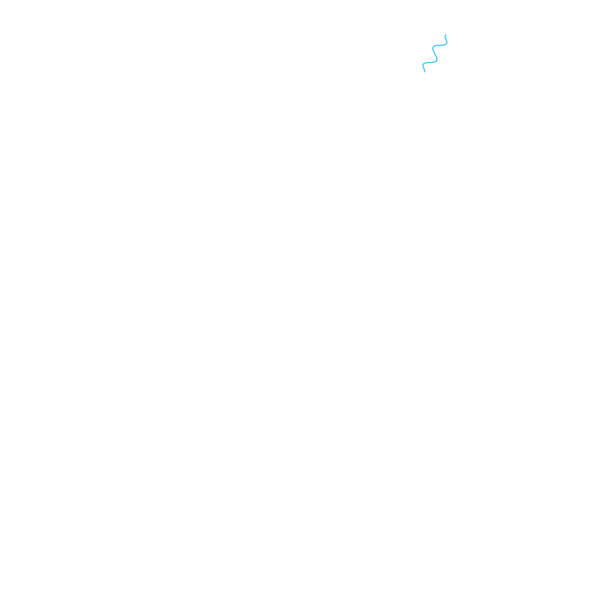
Consider the diagram above, in which a body is in tangential motion with respect to the surface of the Earth. As , we can describe as just . This leaves us with

Expanding equation gives

Recall from the section on the time derivative equivalent, is equivalent to the number of pseudo-time derivatives in 1 unit of time, proportional to and . In turn, should be equivalent to . of course can be rewritten as the product of the velocity of the gravitational source and the gradient of spatial dilation dilation, .

This then gives

And then simplifying equation and solving for gives

If we then substitute our standard orbital velocity formula for we find

Relativistic center of mass shift

Consider the diagram in figure above. Recall that in the model being proposed, velocity derivatives should be proportional to some , the displacement derivative of a magnitude equivalent to the speed of light. This is to say that for some infinitesimally small , .

We can then define as follows:

We then find for where is the standard gravitational acceleration of :

Let us then recognize that must be proportional to . As we find

What this transcendental quantity implies is not yet well understood, but the occurrence of in black hole dynamics and the Earth-Moon radius relationship suggests that the appearance of here shouldn't be immediately attributed to mere coincidence. As in the purely mathematical context is defined as an infinite series with several unique properties, there exists an incredible potential for this quantity to tell us more about the nature of gravity and this proposed density axis.

Discussion

While this model is undeniably bold and will certainly be controversial, the proposed model is consistent with every experimental validation of SR and GR, and merely expands upon core concepts contained within the holographic principle and emergent gravity models to produce the physical description of space-time through space and motion alone. The model so closely mirrors the original work of Einstein, producing numerically equivalent results in the majority of cases, finding ways to distinguish this model from existing interpretations of relativity proved far more challenging than fitting existing experimental data.

While this model will and should be met with a high degree of skepticism, I believe the results speak for themselves. Among other phenomena that fall out of this model, there now exists the concept of a temporal plane, a spherical 'surface' of an equal spatial density, giving a new equi-potential of sorts. Combining this model with electromagnetism opens the door to a new interpretation of electric charge, and provides an opportunity to more completely unify the electromagnetic field and potentially bind the electromagnetic field with gravity. When considering the notion of a new equi-potential with the fact that the proposed spatial gradient along an infinitesimally small radius, , gives the symmetry:

Further, this model describes the apparent gravitational acceleration as the relative motion of space, not the observer in apparent free fall. This model gives with respect to space for the observer in apparent free fall as the relative motion is now applied to space itself, making , which directly addresses the fruitless search for the graviton.